Coursera | deeplearning.ai | Andrew Ng (1-3)--浅层神经网络
神经网络和深度学习—浅层神经网络
CSDN -吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-3)– 浅层神经网络-作者: 大树先生
4. 激活函数的选择
几种不同的激活函数 $g(x)$:
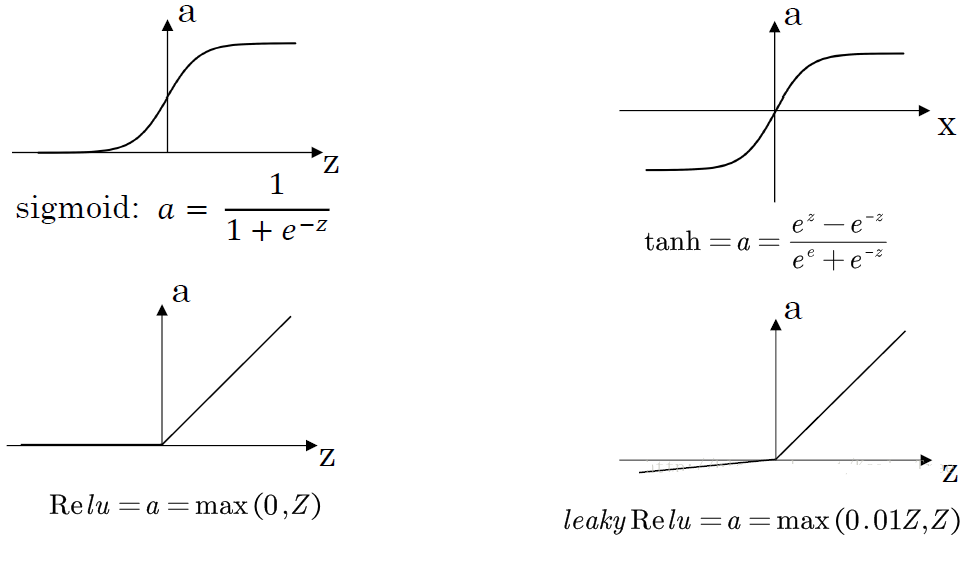
sigmoid:$a = \dfrac{1}{1+e^{-z}}$
导数: $a’ = a(1-a)$
tanh:$a=\dfrac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$
导数:$a’=1-a^{2}$
ReLU(修正线性单元):$a = \max(0,z)$
Leaky ReLU:$a = \max(0.01z,z)$
激活函数的选择:
sigmoid函数和tanh函数比较:
隐藏层:$tanh$ 函数的表现要好于 $sigmoid$ 函数,因为 $tanh$ 取值范围为[−1,+1],输出分布在 0 值的附近,均值为 0,从隐藏层到输出层数据起到了归一化(均值为 0)的效果。
输出层:对于二分类任务的输出取值为 { 0 , 1 },故一般会选择 $sigmoid$ 函数。
然而 $sigmoid$ 和 $tanh$ 函数在当 |z| 很大的时候,梯度会很小,在依据梯度的算法中,更新在后期会变得很慢。在实际应用中,要使 |z| 尽可能的落在 0 值附近。
$ReLU$ 弥补了前两者的缺陷,当 z>0 时,梯度始终为 1,从而提高神经网络基于梯度算法的运算速度。然而当 z<0 时,梯度一直为 0,但是实际的运用中,该缺陷的影响不是很大。
$Leaky -ReLU$ 保证在 z<0 的时候,梯度仍然不为 0。
在选择激活函数的时候,如果在不知道该选什么的时候就选择 $ReLU$,当然也没有固定答案,要依据实际问题在交叉验证集合中进行验证分析。
$F_a = F_b + F_c + F_{\mu}$
[
]