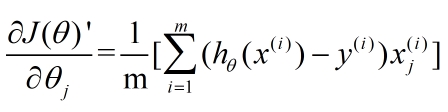Logistic回归-代价函数求导过程 | 内含数学相关基础
相关函数求导公式
先复习回顾下一些数学基础,帮助推导过程可以更好的理解。下面列举的公式都是,接下来的推导中会用到的,没有涉及到的公式,此处不再列举。
- 常数项求导
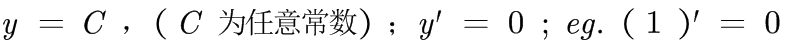
- 以 e 为底的指数求导公式
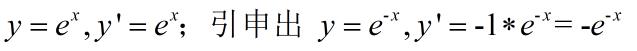
- 对数复合求导公式
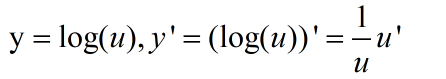
- 幂函数复合求导公式
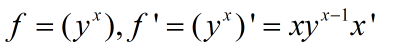
- 函数的和、差、积、商的求导法则
设 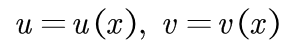 ,都可导,则
,都可导,则
(1) 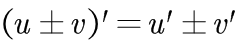
(2) 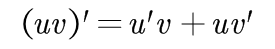
(3) 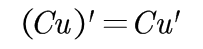
(4) 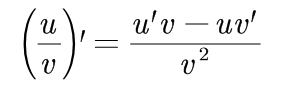
复合函数求导法则
设 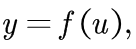 而
而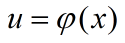 且
且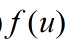 及
及 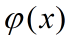 都可导,则复合函数
都可导,则复合函数 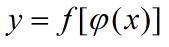 的导数为
的导数为
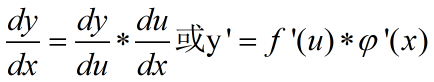
Logistic 回归的 Cost function 的推导过程:
之前采用的是梯度下降算法用来求函数的最小值。
好吧,来吧正式开始了,有了以上的数学求导基础,接下来就容易多了,公式嘛,当初上学时,老师常说的一句话:“背过,记住!”
Logistic回归的代价函数可以统一写成如下一个等式:
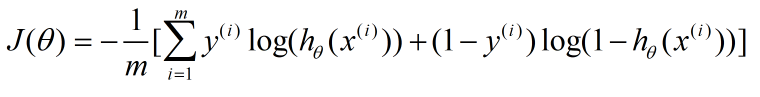
其中: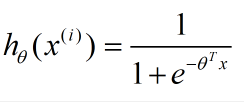
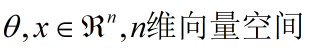
下面开始我们的推导过程:如果要求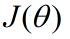 对某一个参数
对某一个参数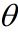 的偏导数,则:
的偏导数,则:
- 1.根据求导公式,可以先把常数项
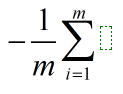 提取出来,这样就只需要对求和符号内部的表达式求导,即:
提取出来,这样就只需要对求和符号内部的表达式求导,即:
(1) 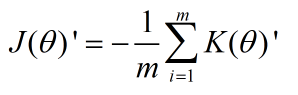
其中 K(θ)’ 为:
(为方便显示,先把右上角表示第i个样本的上标去掉)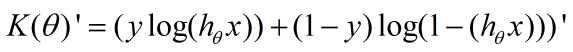
- 2.根据对数复合求导公式,
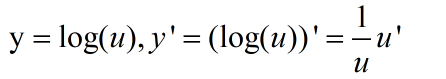 ,对 K(θ)’ 继续求导可得:
,对 K(θ)’ 继续求导可得:
(2) 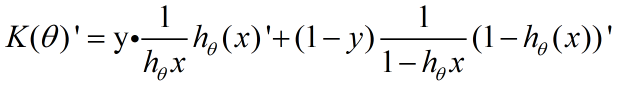
之后 需要对 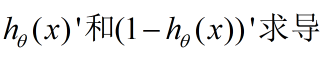
现在 根据上面提到的
- 幂函数复合求导公式
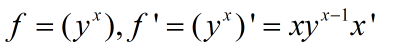
- 以 e 为底的指数求导公式
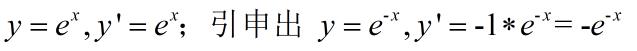
先对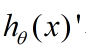 求导:
求导:
根据上面的已知公式:
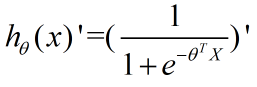
依据上面的商求导公式可得:


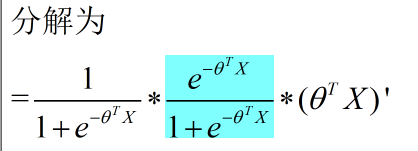
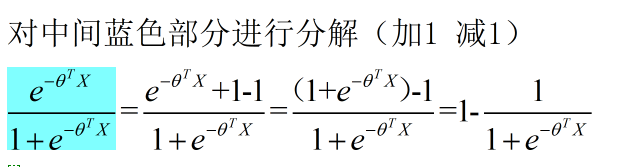
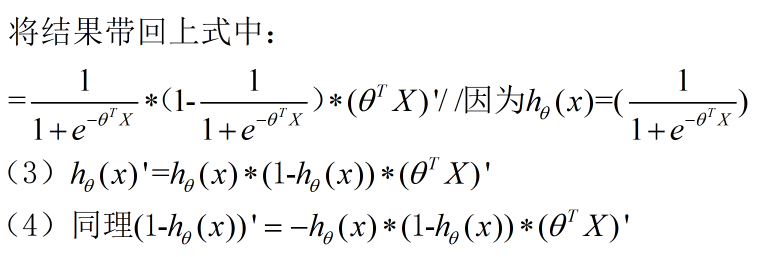
将 (3) (4) 代入 (2) 中 ,可得:
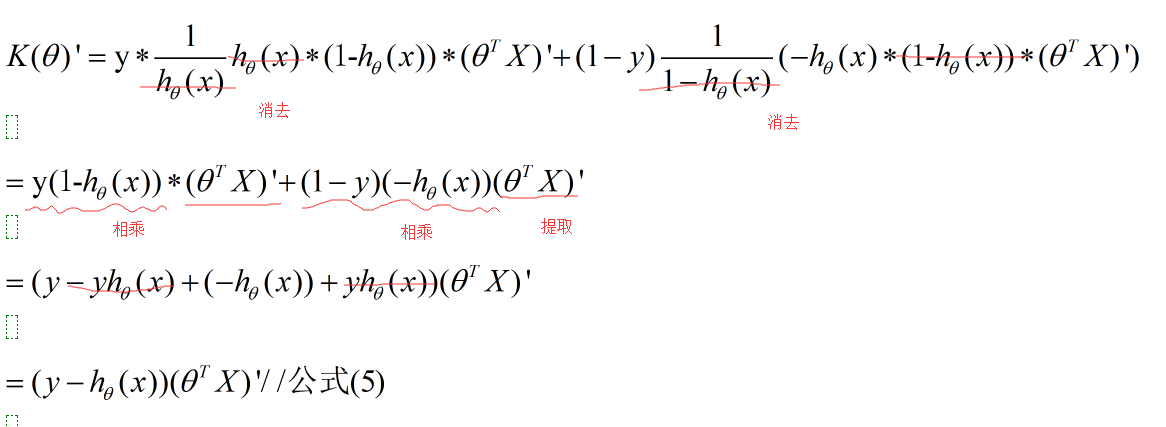
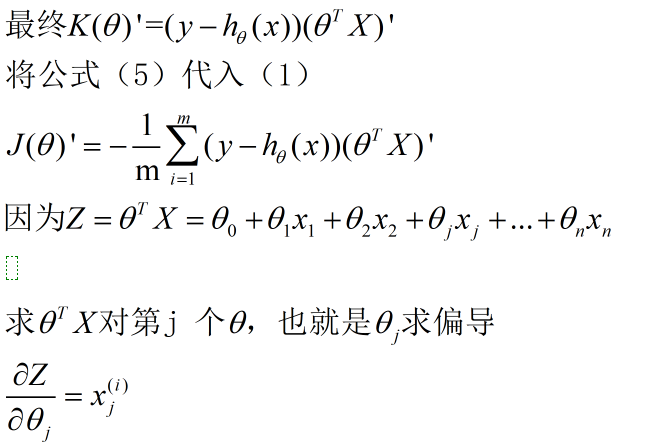

推导结果: